-
Автотовары
-
Сантехника, ремонт, вентиляция
- Увлажнители воздуха
- Метеорологические станции, термометры
- Осушители воздуха, влагопоглотители
- Вентиляторы для ванной
- Эфирные масла для диффузора
- Вентиляторы
- Аксессуары для вентиляционного оборудования
- Очистители воздуха
- Кондиционеры, рекуператоры
- Механические инструменты
- Электроинструменты
- Ящики для инструментов, держатели
- Крепежные изделия
- Стеллажи, полки
- Стремянки
- Складные системы для полок
- Лопаты для снега, толкатели
- Металлодетекторы
- Снегоуборщики
- Платформенные весы
- Моющее оборудование высокого давления
- Камеры видеонаблюдения
- Дверные звонки, глазки
- Системы безопасности, контроллеры
- Датчики
- Детекторы дыма, газа
- Домофоны
- Cигнализации
- Принадлежности для систем безопасности
- Выключатели, розетки
- Зарядные устройства для элементов питания
- Батарейки
- Светодиодные ленты
- Фонарики, прожекторы
- Удлинители
- Электрические лампы
- Таймеры, термостаты
- Комплектующие для солнечных электростанций
- Источник питания
- Текстильные провода и клеммные колодки
- Монтируемые светильники, светодиодные панели
-
Подарки, праздничная атрибутика
-
Товары для детей и младенцев
- Для ухода за младенцем
- Приспособления для кормления
- Товары для мам
- Детские коляски и аксессуары
- Автокресла и аксессуары к ним
- Манежи для детей
- Шезлонги и качели
- Детское питание
- Ходунки
- Слинги, эргорюкзаки
- Отпечатки для младенцев
- Матрасы для новорожденных
- Подгузники
- Детские кроватки
- Детское постельное бельё
- Приданое для новорожденного
- Товары для безопасности детей дома
- Одежда для новорождённых
-
Духи, косметика
- Средства для маникюра и педикюра
- Помады, бальзамы, блеск для губ
- Косметички, косметические зеркала
- Кисти для макияжа, спонжи
- Пудры, базы под макияж
- Тушь, средства для роста ресниц, тени для век, карандаши для глаз
- Лаки, укрепители для ногтей
- Накладные ресницы, керлеры
- Карандаши, краска для бровей
- Бронзеры (бронзаторы), румяна
- Кремы для лица
- Средства для очищения лица
- Маски для лица, патчи для глаз
- Массажеры для лица, инструменты для чистки лица
- Сыворотки для лица, масла
- Сыворотки, кремы для век
-
Мебель и домашний интерьер
- Комплектующие для кухонной мебели
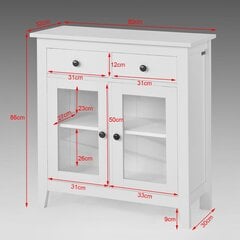
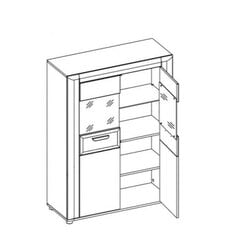
- Кухонные шкафчики
- Стулья для кухни и столовой
- Кухонные и обеденные столы
- Кухонные гарнитуры
- Комплекты мебели для столовой
- Столешницы для кухни
- Коллекции кухонной мебели
- Комплекты в ванную
- Шкафчики для ванной
- Зеркала в ванную
- Полки для ванной
- Аксессуары для ванной комнаты
- Коллекции мебели для ванной
- Детские кровати
- Детские диваны, кресла
- Детские матрасы
- Полки для книг и игрушек
- Комплекты для детской комнаты
- Детские столы и стулья
- Детские кроватки
- Детские комоды
- Детские шкафы
- Шкафчики в детскую
- Детские письменные столы
- Стулья для школьников
- Коробки для игрушек
- Коллекции мебели для детской комнаты
-
Бытовая техника и электроника
- Кофемолки
- Кофемашины
- Электрочайники
- Фритюрницы
- Фильтры для воды
- Весы (кухонные)
- Блендеры, измельчители
- Вафельницы и электрические блинницы
- Особенные приборы для приготовления пищи
- Ломтерезки, точилки для ножей
- Миксеры
- Бутербродницы
- Соковыжималки
- Вакууматоры
- Мультиварки
- Электрогрили, маринаторы
- Кухонные комбайны
- Тостеры
- Коктейльницы
- Проращиватели, лампы для растений
- Аппараты для газирования воды
- Мясорубки
- Сушилки для фруктов
- Аппараты для воды
- Хлебопечки
- Пылесосы
- Пылесосы-роботы
- Беспроводные пылесосы
- Моющие пылесосы
- Весы (бытовые)
- Пароочистители, оборудование для мытья полов
- Роботы для мытья окон, стеклоочистители
- Аккумуляторы для пылесосов
- Аксессуары для пылесосов
- Метеорологические станции, термометры
- Приборы для укладки и выпрямления волос
- Массажеры
- Электробритвы
- Электрические зубные щетки
- Фены
- Эпиляторы
- Согревающие приборы
- Аппараты для маникюра и педикюра
- Машинки для стрижки волос
- Насадки для электрических зубных щеток
- Ирригаторы
- Тонометры
- Приборы для ухода за лицом
- Ингаляторы
- Массажные ванночки
- Термометры
- Вентиляторы
- Кондиционеры, рекуператоры
- Обогреватели
- Увлажнители воздуха
- Водонагреватели
- Нагревательные коврики для пола и зеркал
- Вентиляторы для ванной
- Детекторы дыма, газа
- Аксессуары для вентиляционного оборудования
-
Компьютерная техника
- Аксессуары для корпусов
- Внутренние жёсткие диски (HDD, SSD, Hybrid)
- Оперативная память (RAM)
- Корпуса
- Контроллеры
- Аксессуары для компонентов
- Компьютерные вентиляторы
- Блоки питания (PSU)
- Материнские платы
- Видеокарты (GPU)
- Кулеры для процессоров
- Термопасты
- Оптические устройства
- Процессоры (CPU)
- Водяное охлаждение - аксессуары
- Водяное охлаждение - комплекты
- Кулеры для видеокарт
- Звуковые карты
- ТВ-тюнеры, FM, видеокарты
-
Мобильные телефоны, Фото и Видео
- Чехлы для телефонов
- Защитные пленки для телефонов
- Аксессуары для телефонов
- Мобильные телефоны
- Держатели для телефонов
- Зарядные устройства для телефонов
- Зарядные устройства Power bank
- Кабели для телефонов
- Карты памяти для телефонов
- Запчасти для телефонов и инструменты для их ремонта
- Моноподы для селфи («Selfie sticks»)
- Аккумуляторы для телефонов
- Беспроводная гарнитура
- Наушники
- Аксессуары для фотоаппаратов
- Осветительное оборудование для фотосъемок
- Цифровые фотоаппараты
- Фотоаппараты мгновенной печати
- Карты памяти для фотоаппаратов, камер
- Футляры, чехлы для фотоаппаратов и объективов
- Зарядные устройства для фотоаппаратов
- Штативы для фотоаппаратов
- Аккумуляторы для фотоаппаратов
- Объективы
- Фильтры для объективов
- Заряжаемые батарейки
-
Одежда, обувь и аксессуары
-
Спорт, досуг, туризм
- Туристический инвентарь
- Фляги для воды
- Туристические, походные рюкзаки
- Альпинистское снаряжение
- Палатки
- Туристические матрасы и коврики
- Надувные матрасы и мебель
- Спальные мешки
- Средства для ухода за обувью, одеждой и туристическим инвентарём
- Туристическая мебель
- Биотуалеты
- Принадлежности для автотуризма
- Средства защиты от комаров
- Товары для гимнастики и фитнеса
- Рюкзаки и сумки
- Аксессуары для массажа
- Футбол
- Водный спорт
- Ракеточный спорт
- Ортезы и бандажи
- Баскетбол
- Боевые искусства
- Палки для ходьбы
- Гольф
- Дартс
- Шагомеры, хронометры, мониторы сердечного ритма
- Сетевой
- Диск-гольф
- Товары для балета и гимнастики
- Насосы и иглы для мячей
- Ручное
- Бейсбол
- Верховая езда
- Флорбол и хоккей на траве
- Велосипеды, ролики, скейтборды
- Грузы, гантели, грифы
- Игровые столы
- Тренажеры, товары для фитнеса
- Мячи
- Аминокислоты
- Углеводы
- Протеин
- Батончики
- Другие пищевые добавки и препараты
- Энергетики
- Функциональные продукты
- Глютамин
- Креатин
- L-карнитин
- Пищевые добавки и препараты для набора массы
- Добавки и препараты для суставов
- Добавки для восстановления
- Жиросжигатели
- Добавки и препараты для похудения
- Стимуляторы тестостерона
- Витамины
-
Кухонные товары, товары для домашнего хозяйства
- Кухонная утварь
- Формы, посуда для выпечки
- Стаканы, фужеры, кувшины
- Посуда, тарелки, обеденные сервизы
- Посуда для хранения еды
- Кастрюли, скороварки
- Ножи и аксессуары для них
- Cковородки
- Термосы, термокружки
- Столовые приборы
- Чайники, кофейники
- Емкости для специй, измельчители
- Разделочная доска
- Специи, наборы специй
- Посуда и принадлежности для консервирования
- Фляги, бутылки для воды
- Одноразовая, тематическая посуда
- Фильтры для воды
-
Товары для животных
- Игрушки для собак
- Переноски, сумки
- Миски, ящики для корма
- Одежда для собак
- Лежаки, домики
- Сухой корм для собак
- Средства по уходу за животными
- Дорожные принадлежности
- Лакомства для собак
- Ошейники, подтяжки для собак
- Поводки для собак
- Консервы для собак
- Витамины, добавки, средства от паразитов для собак
- Косметические средства для животных
- Средства для дрессировки собак
- Игрушки для кошек
- Когтеточки
- Сухой корм для кошек
- Туалеты для кошек
- Консервы для кошек
- Наполнители для кошачьих туалетов
- Лакомства для кошек
- Витамины, добавки и средства от паразитов для кошек
- Поводки и ошейники для кошек
- Лежаки, домики
- Переноски, сумки
- Миски, ящики для корма
- Косметические средства для кошек
- Средства по уходу за кошками
-
Товары для сада
- Запчасти для садовой техники
- Пылесосы для сбора листьев, измельчители веток, очистители тротуарной плитки
- Газонокосилки
- Триммеры
- Психрометры, термометры, измерители pH, ORP
- Кусторезы, ножницы для газона
- Тележки
- Роботы-газонокосилки
- Дровоколы
- Культиваторы, мотоблоки, аэраторы
- Садовые тракторы
- Садовые земляные буры
- Подметальные машины
-
Книги
-
Защитные, дезинфицирующие средства, медицинские товары
- Маски pеспираторы
- Защитные стенки, дозаторы для антисептика
- Дезинфицирующие средства
- Одноразовые перчатки
- Дезинфицирующие чистящие средства
- Защитные очки, экраны для лица
-
Эротические товары
n18.lt специализированный магазин для взрослых
Товары в специализированном магазине для взрослых n18.lt могут видеть только посетители не младше 18 лет. Информация, распространяемая на данной веб-странице, может оказывать негативное воздействие на лиц младше 18 лет.Посмотреть товары - Продукты питания
-
Умный дом
- Аутлет
-
Товары для офиса, школы, творчества
Показать больше категорий

 Счастливых праздников! Дополнительно -5€ на заказы свыше 100€ с кодом* 5XMAS1224
Счастливых праздников! Дополнительно -5€ на заказы свыше 100€ с кодом* 5XMAS1224